Articles
Understanding Fan Performance Curves
introduction
One of the most important documents that customers request from fan manufacturers is performance curves. In addition to graphically depicting basic fan performance data for CFM, RPM, SP (on a static pressure curve) and BHP (on a brake horsepower curve), these curves also illustrate the performance characteristics of different fan types, such as areas of instability, or the rate of change between flow and pressure. With some basic knowledge of performance curves, decisions can be made about fan selection, fan and system modifications, or the desirability of using a fan in a modification system, for example. Except for very large fans, performance curve information is generated by connecting the fan to a laboratory test chamber. Very specific test procedures as specified in Air Motion and Control Association Standard 210 are followed to ensure uniform and accurate readings. Data points are collected at a specific RPM while flow is slowly adjusted from fully closed to fully open. The information gathered is then used to develop computer selection programs and published capacity tables for use by system designers and end users.
Static Pressure Curve
The static pressure curve provides the basis for all flow and pressure calculations. This curve is created by plotting a series of static pressure points against specified flow rates at a given test speed. While the static pressure curve depicts the performance of a fan at a given speed, it can be used to determine the fan’s ability to produce pressure at any volume. In addition, it is also possible to approximate fan performance at other speeds by applying the following fan laws:
CFM varies with RPM
SP varies with (RPM)2
BHP varies with (RPM)3
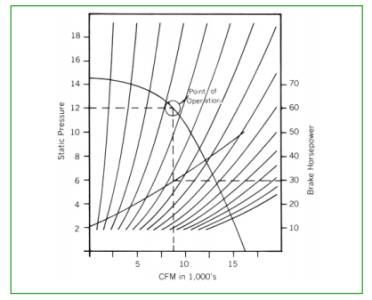
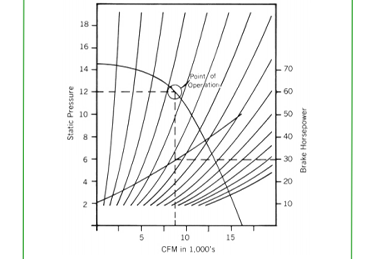
To determine the fan’s operating point, first determine the desired static pressure on the SP scale to the left of the curve. Then draw a horizontal line to the right, to the point of intersection with the SP curve. Next, draw a vertical line from the operating point to the CFM scale at the bottom to determine the fan’s flow capacity for that SP at the specified speed. As shown in Figure 1, the performance of this fan is 8750 CFM and 12″ SP at 1750 RPM. Assuming this same fan was intended to operate at 1200 RPM, the fan laws can be applied to obtain performance at this lower speed.
.
- CFM varies as RPM
CFM (new) /CFM (old)=RPM (new)/RPM (old)
Therefore:
CFM (new) =1200/1750(8750) = 6000 CFM
- SP varies as (RPM)2
SP (new)/ SP (old)=(RPM (new)/ RPM (old) )2
Therefore:
SP (new) =( 1200/1750)2 (12) = 5.6” SP
Brake horsepower curve
Once the CFM and SP are determined, the BHP rating can be determined. An accurate BHP rating is essential to properly size a motor or to determine the operating efficiency of one fan compared to another. Performance curves contain a BHP curve from which the BHP rating for a given capacity can be determined. To determine the BHP at a given operating point, a horizontal line is drawn to the right of the point of intersection of the vertical CFM line and the BHP curve.

- BHP varies as (RPM)3
BHP (new)/BHP (old)=(RPM (new)/ RPM (old) )3
Therefore:
BHP (new) =(1200/1750)3 (30) = 9.67 BHP
System lines
Since fans are tested and evaluated independently of any type of system, a means must be provided to determine the fan capabilities within a given system. Fan laws apply equally to any system; therefore, variations in CFM and SP within a system are predictable. This allows system lines to be superimposed on performance curves to simplify performance calculations. A system line is nothing more than the sum of all possible CFM and SP combinations within a given system. Any combination of fan and system must operate somewhere along this system line. Since the fan must operate somewhere along its SP curve and the system has a known system line, their intersection is the operating point. If the fan speed changes, the operating point must move up or down the system line. If the system changes in some way, the operating point must move up or down the SP curve. In practice, these principles can be used to verify the accuracy of fan performance and system design..
Using performance curves
Figure 3 shows a fan operating point selected for an 8750 CFM, 12-inch SP running at 1750 RPM. Figure 3 includes a number of different system lines. If the system is not operating properly at startup, measurements can be taken and compared to the available performance curve.
Suppose the tachometer reading indicates that the fan is running at 1200 rpm instead of 1750 rpm, due to errors in motor speed or motor selection, and the airflow check indicates only 6000 cfm. These readings confirm that the system is correctly calculated and that the fan speed should be corrected to 1750 rpm as originally specified to achieve the required 8750 cfm. If the tachometer reading indicates the proper speed but the airflow reading is low, additional system resistance beyond that originally calculated is indicated. This additional resistance can be caused by partially closed vents/dampers, changes in duct size from the original design, system impact losses, or simply an error in the system resistance calculations. The deficiency can usually be corrected by either changing the system or increasing the fan speed. Often, single speed performance curves should be used to determine fan performance for use in systems that require more air or higher pressures. A performance curve such as Figure 4 can be used to determine fan performance beyond the SP scale shown using the fan laws to obtain a reference point for on-line operation. This can be accomplished by applying some appropriate factor to the required CFM and squaring this factor to the required SP. For example, the performance curve shown in Figure 4 can be used to determine the fan performance requirements for a system calculated at 15,000 CFM and 23.5″ SP, even if this point is outside the curve. By determining an appropriate reference capacity using the fan laws, which falls within the curve data, the fan performance requirements at the curve speed can be obtained and then projected to the system requirements using the fan laws again.
There is a 15,000 CFM and 23.5″ SP required on the same system as a 10,000 CFM at 10.4″ SP which intersects the fan SP curve plotted at 1750 RPM and has a corresponding BHP of 33.0 at 1750 RPM. Therefore:
RPM (new) =1500/1000 (1750) = 2625 RPM
BHP (new) =(1500/1000)3 (33.0) = 111 BHP
Fan performance characteristics
Fan performance characteristics can be determined by the performance curve at a glance. These characteristics include things like stability, increased or no increase in thrust, and acceptable operating points. Fan performance is based on certain flow characteristics as air passes over the fan wheel blades. These flow characteristics are different for each general fan or wheel type (i.e. radial, forward-bent, backward-bent, radial tip, and axial). Therefore, the performance characteristics will be different for each of these general fan types. Furthermore, these performance characteristics may vary from manufacturer to manufacturer depending on the particular design. The characteristics shown in this message are based on NYB fan equipment.
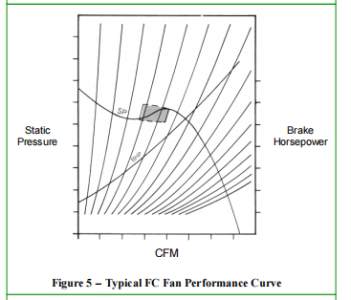
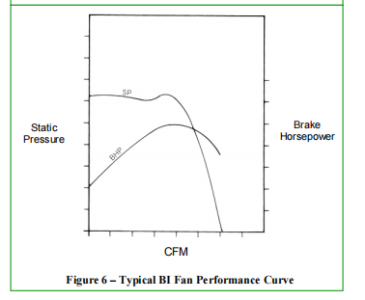
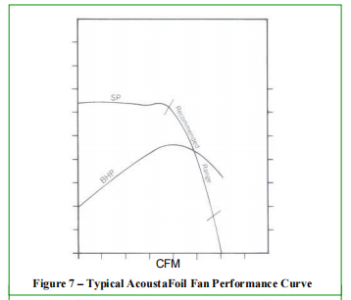
The performance curves shown in Figures 1 through 4 are typical of radial-bladed wheel fans. The SP curve is smooth and stable from wide open to closed. The BHP curve clearly indicates that BHP increases steadily with the volume of air handled as shown in Figure 4. Forward-curved wheel fans, as shown in Figure 5, also have a BHP curve that increases with the volume of air handled. The SP curve differs significantly from the radial curve in that it shows a sharp “slope” to the left of the peak static pressure. This sharp slope (shaded area) indicates unpredictable flow characteristics. Although technically imprecise, this region is often referred to as the “stalling” region. This indicates that at these relatively low pressure and volume combinations, the airflow characteristics across the wheel blades change or break up such that the fan’s performance point is no longer stable. Any fan with this characteristic SP curve should not be selected for operation in the unstable region. As shown in Figure 6, the SP curve for the backward-tilted fan has a steeper slope to the left of the peak static pressure. This indicates a region of instability. However, the backward-tilted SP curve is generally steeper than the forward-tilted wheel curve, indicating its desirability for use in higher pressure systems. Therefore, differences in system resistance will result in smaller volume changes for the BI fan when compared to the FC fan. Although New York Blower centrifugal fans with AcoustaFoil® wheels are stable in the left-of-peak region, the majority of fans with backward-tilted wheels exhibit an SP curve similar in appearance to that of the forward-tilted fan. The SP curve shown (in Figure 7) for fans using AcoustaFoil wheels (airfoil, backward-tilted) exhibits a smoother decline to the left of the peak static pressure. This indicates that the overall design of the fan is such that the internal flow characteristics remain desirable or expected even in the left-of-peak region and that performance in this region is stable.
The BHP curve for all back-tilted fans is the main difference between them and all other types of fans. As shown in Figures 6 and 7, the BHP curve for back-tilted fans peaks and then decreases as the fan size increases. Thanks to this “non-overload” BHP property, it is possible to determine the maximum BHP for a given fan speed and select a motor that will not be overloaded despite any changes or errors in the system design. Because BHP varies with RPM3, this non-overload property does not apply to increases in fan speed, but it is very useful for protecting the motor from errors or changes in system calculations and installation. Figures 5 and 6 indicate certain unacceptable selection regions on the SP curve. Although stability or performance may not be a problem, the operating point to the far right of the SP curve should be avoided. Choosing a fan that operates to the far right eliminates the flexibility needed to compensate for future system changes. The fan is also less efficient in this region than a larger fan operating at a slower speed. Figure 7 shows the best selection region on the SP curve and the region where the majority of capacity tables are published. As shown in Figure 8, the radial tip fan design combines the characteristics of the back-sloping SP curve and the
BHP for Radial Fan. Radial tip fans are often more efficient than radial fans and are generally best applied to high pressure applications. Due to their efficiency and dust handling capabilities, radial tip fans can also be applied to low pressure material conveying systems.
BHP for Radial Fan. Radial tip fans are often more efficient than radial fans and are generally best applied to high pressure applications. Due to their efficiency and dust handling capabilities, radial tip fans can also be applied to low pressure material conveying systems.
conclusion
A good knowledge of performance curves is essential to understanding the performance characteristics and capabilities of different fan equipment. Using performance curves in selecting fan types and sizes will ensure stable and efficient operation as well as future flexibility.